中2数学の要！一次関数と連立方程式を同時克服する勉強法を徹底解説

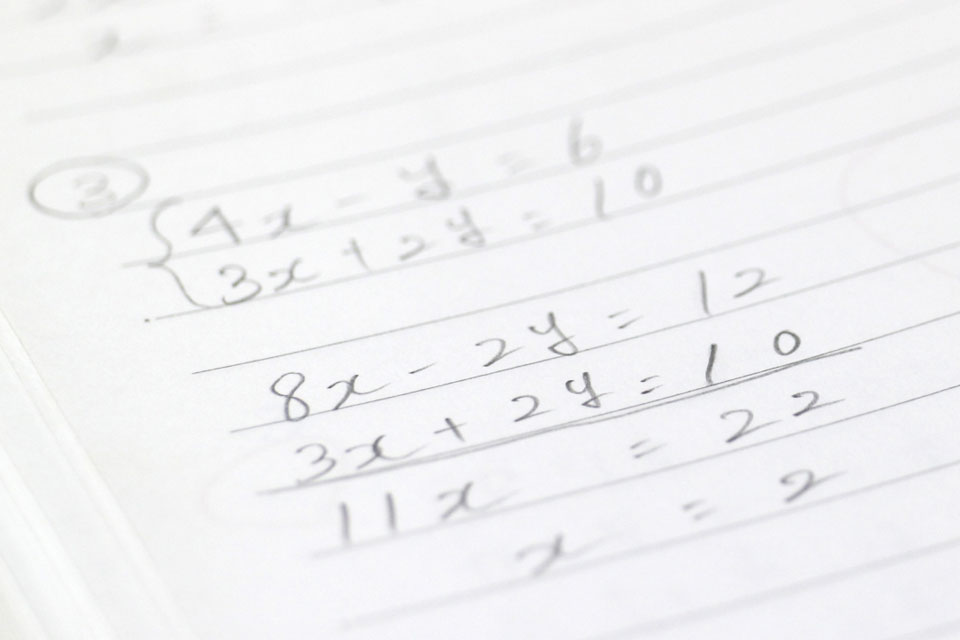
中学2年生の数学で多くの生徒が苦戦する「一次関数」と「連立方程式」。

この2つの単元は、実は密接に関係しており、別々に勉強するよりも同時に学習することで効率よく理解できることをご存知でしょうか。

この2つについて多くの中学生が「グラフが描けない」「式の意味がわからない」「文章題から式が立てられない」という悩みを抱えています。
しかし、これらの悩みは正しく理解して勉強することで解決できるようになります。

この記事では、一次関数と連立方程式を同時に克服するための具体的な勉強法を、つまずきやすいポイントとその解決策とともに詳しく解説します。
こうした勉強法をマスターすれば、中2数学の土台がしっかりと固まり、中3の二次関数や高校数学への準備も整います。

数学に対する苦手意識を持っている皆さんも、きっと「わかった！」という実感を得られることでしょう。

「一次関数」と「連立方程式」で大切なのはなに？

1年生で学んだ「比例・反比例」が土台になる

中1で学習した比例・反比例は、一次関数の基礎となる重要な概念です。
比例の式y = axは、実は一次関数y = ax + bのbが0の特別な場合となります。
つまり、比例を理解していれば一次関数の理解はぐっと楽になります。

比例で学んだ「変化の割合が一定」という性質は、一次関数の「傾きが一定」という概念につながっています。
また、座標平面上に点を打ったり、グラフを読み取ったりするスキルも、一次関数のグラフを扱う際に直接活用されます。

もし比例・反比例に不安がある場合は、一次関数の学習前に必ず復習しておきましょう。
特に、xの値が2倍、3倍になったときのyの値の変化や、グラフの特徴を再確認することが大切です。

「式」と「グラフ」、2つの考え方を同時に使おう！

数学の力は、問題を多角的に見る能力にあります。
一次関数と連立方程式を学ぶことで、同じ問題を「式」と「グラフ」の両方から考えられるようになります。

例えば、2つの一次関数の交点を求める問題では、連立方程式を解いて座標を計算する方法と、実際にグラフを描いて交点を読み取る方法があります。
どちらのアプローチも使えるようになることで、問題への理解が深まり、検算もしやすくなります。

また、グラフで視覚的に理解したことを式で表現したり、逆に式から得られる情報をグラフで確認したりする習慣がつくと、数学的なセンスが格段に向上します。

3年生の二次関数にもつながる、数学の基本が詰まった単元

3年生の二次関数にもつながる、数学の基本が詰まった単元です。
一次関数で学ぶ概念は、中3で学ぶ二次関数の土台となります。

関数の考え方、グラフの読み方、変化の割合の理解、そしてグラフから数の増減を読み取る力など、すべてが二次関数の理解につながっています。

また、関数とグラフの関係を理解しておくことで、物理や化学といった理科の分野でも、グラフを読み解く力を発揮できます。

つまり、中2のこの時期にしっかりと基礎を固めておくことで、数学だけでなく理系科目全体に良い影響を与えることができるでしょう。

まずは違いとつながりを整理しよう｜一次関数と連立方程式

変化のある関係をグラフで表すのが一次関数

一次関数は、2つの量の間の関係を表現する数学的な道具です。
y = ax + bという式で表され、xの値が変わるとyの値がどのように変化するかを示しています。

重要なのは「変化」の概念です。

例えば、タクシー料金の計算では、基本料金（切片b）に加えて、距離に応じて一定の割合（傾きa）で料金が増加します。

このような身近な例を通じて、一次関数の意味を理解することが大切です。

たとえば「傾きが2で、切片が−1」のように2つの値が決まると、その直線は1つに決まります。
一次関数では、この「傾き」と「切片」がとても大事なポイントになります。

2つの条件から同時に答えを求めるのが連立方程式

連立方程式は、複数の条件を同時に満たす解を求める手法です。

例えば、「りんご3個とみかん2個で500円、りんご2個とみかん4個で600円」という2つの条件から、りんごとみかんそれぞれの値段を求める場合に使用します。

2つの式を組み合わせることで、1つの式では求められない未知数の値を特定できるのが連立方程式の特徴です。
解法には加減法と代入法がありますが、どちらも「一方の文字を消去して、もう一方の文字の値を求める」という基本原理は同じです。

重要なのは、連立方程式の解が「2つの条件を同時に満たす唯一の組み合わせ」であることを理解することです。
この理解があれば、検算の際にも両方の式に代入して確認する習慣が身につきます。

どちらも「一次式」！交点＝共通の解という関係に注目

一次関数と連立方程式の最も重要な関係は、2つの一次関数のグラフの交点が、それらの式から作られる連立方程式の解になることです。
この関係を理解すれば、問題解決の幅が大きく広がります。

例えば、y = 2x + 1とy = -x + 7という2つの一次関数があるとき、これらのグラフの交点の座標は、連立方程式2x + 1 = -x + 7を解くことで求められます。
逆に言えば、連立方程式の解をグラフ上で視覚的に確認することもできるという解釈になります。

この関係性を理解することで、「式で計算した答えをグラフで確認する」「グラフで大まかな答えを予想してから式で正確に計算する」といった柔軟な問題解決が可能になります。

どこでつまずく？よくある悩みとその理由

「傾き」や「切片」があいまいなまま、グラフだけ描いていない？

多くの生徒が陥りがちなのが、傾きや切片の意味を理解せずに、パターン暗記でグラフを描こうとすることです。
これでは応用問題に対応することが難しくなります。

傾きaは「xが1増加したときのyの増加量」であり、グラフ上では直線の傾き具合を表します。
正の値なら右上がり、負の値なら右下がりになります。
また、切片bはx = 0のときのyの値で、グラフではy軸との交点を表します。

これらの意味を理解せずにグラフを描くと、問題文から式を立てることができなくなります。

例えば、「毎分3cmの速さで水が増える」という文章を見たときに、これが傾き3を意味することがわからなくなってしまいます。

加減法と代入法、どっちを使えばいいかわからない！

連立方程式の解法選択で迷う生徒も多くいます。
実は、どちらの方法でも必ず解けますが、問題によって効率の良い方法が異なります。

加減法は、係数を揃えて足し引きすることで文字を消去する方法です。
係数が小さい整数で揃えやすい場合や、既に係数が同じ（または互いに逆数）の場合に威力を発揮します。

代入法は、一方の式から片方の文字について解き、それをもう一方の式に代入する方法です。
係数が1の文字がある場合や、一方の式が既に解かれた形になっている場合に適しています。

慣れてくれば、問題を見た瞬間にどちらが効率的か判断できるようになるでしょう。

式とグラフがつながらないと、問題の意味が見えなくなる

最も深刻な問題は、式とグラフを別々の知識として覚えてしまうことです。
これでは、問題の本質を理解することができません。

例えば、「2つの直線の交点を求めよ」という問題を見たときに、「交点の座標を求める」＝「連立方程式を解く」という関係性が見えないと、何をすればよいかわからなくなります。

また、文章題では問題の状況をグラフで表現できると理解が深まりますが、式とグラフがつながっていないとこの視覚化ができません。

結果として、暗記頼みの勉強になってしまい、少し問題のパターンが変わるだけで解けなくなってしまいます。

「グラフと式を行き来する力」をつけよう！同時克服のカギ

式からグラフを描いて、傾きや切片の意味を実感しよう

まずは基本の一次関数y = ax + bについて、aとbの値を変えながらグラフを描く練習をしましょう。

例えば、y = 2x + 1、y = 2x – 3、y = -x + 1などを実際に描いてみてください。

傾きが同じ直線は平行になり、切片が同じ直線はy軸上の同じ点を通ることが視覚的に理解できます。
また、傾きが正なら右上がり、負なら右下がりになることも実感できるでしょう。

この練習を通じて、「式の係数や定数項がグラフのどの部分に影響するか」を体感することが重要です。
頭で理解するだけでなく、手を動かして実際にグラフを描くことで、深い理解につながります。

グラフから式を立ててみる｜2点の座標で式をつくる練習

次に、逆の練習として、与えられた2点を通る直線の式を求める練習をしましょう。
これは入試でも頻出の重要なスキルです。

例えば、点(1, 3)と点(3, 7)を通る直線の式を求める場合、まず傾きa = (7-3)/(3-1) = 2を計算します。
次に、点(1, 3)を式y = 2x + bに代入して、3 = 2×1 + bからb = 1を求めます。
よって、求める式はy = 2x + 1となります。

この練習により、グラフ上の情報から式を立てる能力が身につきます。
また、傾きの公式「(yの増加量)/(xの増加量)」の意味も自然に理解できるようになります。

交点を見つけて連立方程式の解を視覚的にとらえよう

2つの一次関数のグラフを同じ座標平面上に描き、その交点を見つける練習をしましょう。
例えば、y = x + 2とy = -2x + 8のグラフを描いて交点を見つけ、その後で連立方程式を解いて座標を正確に求めてみてください。

この練習により、「交点の座標」と「連立方程式の解」が同じものであることが実感できます。
また、グラフを描くことで解の大まかな値を予想でき、計算ミスに気づきやすくなります。

さらに、交点が存在しない場合（平行線）や無数に存在する場合（同じ直線）についても、グラフで視覚的に理解できるようになります。

これらの特殊な場合についても、連立方程式の解の個数と対応させて理解しましょう。

今日からできる！基礎を固める勉強ステップ

「変化の割合」や「比例・反比例」を復習しておこう

まず土台となる中1の内容を確実にしておきましょう。
特に重要なのは変化の割合の概念です。
これは一次関数の傾きの理解に直結します。

比例y = axにおいて、xが2から5に変わったときのyの変化量を求める練習をしてください。
変化の割合は常にaと等しくなることを確認しましょう。
この性質が一次関数でも成り立つことが、一次関数の大きな特徴です。

また、座標平面の使い方、点の座標の読み取り方、グラフの描き方なども復習しておきましょう。

これらの基本技能があやふやだと、その後の学習で大きな障害となります。

グラフを自分の手で描いて、式とセットで覚えるのがコツ

一次関数の学習では、必ず自分の手でグラフを描く習慣をつけましょう。
電卓やパソコンに頼らず、手計算でいくつかの点の座標を求め、それらを結んで直線を描いてみるとよいでしょう。

例えば、y = 3x – 2という式が与えられたら、x = 0, 1, 2, 3のときのyの値を計算し、座標(0, -2), (1, 1), (2, 4), (3, 7)を求めます。

まずは、これらの点をグラフにかきましょう。
次に、それらの点をまっすぐな線で結んで、傾きと切片を確認してみましょう。

この作業を通じて、式とグラフの対応関係が自然に身につきます。
また、グラフから式の特徴を読み取る力も同時に育成されます。

加減法と代入法をどちらも練習！手順に意味を持たせよう

連立方程式では、加減法と代入法の両方をマスターしましょう。
ただし、単純に手順を暗記するのではなく、「なぜその操作をするのか」を常に意識してください。

加減法では、「なぜ係数を揃えるのか」「なぜ足し算や引き算をするのか」を理解しましょう。
これは「同じものを足し引きしても等式は成り立つ」という等式の性質に基づいています。

代入法では、「なぜ一方の文字について解くのか」「なぜ代入するのか」を理解しましょう。
これは「等しいものは置き換えることができる」という数学の基本原理に基づいています。

意味を理解すれば、応用問題でも迷わず解法を選択できるようになります。

式とグラフを同時に使って、「理解できた！」を体感しよう

問題を解く際は、可能な限り式とグラフの両方を活用しましょう。
例えば、連立方程式を解いた後は、必ずグラフを描いて交点の位置を確認してください。

また、文章題では問題の状況をグラフで表現してみましょう。
例えば、「AさんとBさんが異なる速度で歩いている」という問題では、時間を横軸、位置を縦軸にしたグラフを描いて状況を整理すると理解が深まります。

この習慣により、抽象的な数式と具体的な状況の橋渡しができるようになり、数学的思考力が大幅に向上します。

こうした練習を繰り返すことで、「わかった！」という実感を得られる瞬間も増えるでしょう。

応用問題にチャレンジ！実力アップのステップ

文章題から式を立ててグラフを描く練習をしてみよう

実生活に関連した文章題に取り組んでみましょう。

例えば、「入場料500円の遊園地で、乗り物1回につき200円かかる。合計金額yを乗り物の回数xの式で表せ」という問題では、y = 200x + 500という一次関数が立てられます。

この式をグラフに描くことで、乗り物の回数と合計金額の関係が視覚的に理解できます。
また、「3000円持っていたら何回乗れるか」という問題も、グラフ上で y = 3000の直線との交点を見つけることで解決できます。

文章題では、まず状況を整理し、何をx、何をyとするかを明確にすることが重要です。
そして、与えられた条件から式を立て、必要に応じてグラフを描いて関係性を確認しましょう。

日常の中の条件を連立方程式にする力を身につけよう

連立方程式の文章題では、複数の条件を整理して式に表現する力が求められます。

例えば、「大人券と子供券を合わせて10枚買い、合計金額が7000円だった。大人券1枚800円、子供券1枚400円のとき、それぞれ何枚買ったか」という問題を考えてみましょう。

この問題では、大人券をx枚、子供券をy枚とすると、x + y = 10（枚数の条件）と800x + 400y = 7000（金額の条件）という連立方程式が立てられます。

重要なのは、問題文から2つの独立した条件を見つけ出すことです。
また、答えが実際の状況に合っているかの確認も忘れずに行いましょう。

入試でよく出る！関数と連立方程式の融合問題に挑戦

高校入試では、一次関数と連立方程式を組み合わせた問題がよく出題されます。

例えば、「2つの一次関数のグラフが三角形を作るとき、その面積を求めよ」といった問題です。

このような問題では、まず2つの関数の交点を連立方程式で求め、次にx軸やy軸との交点も求めて三角形の頂点の座標を特定します。
その後、座標を使って面積を計算します。

融合問題を解くコツは、問題を小さな部分に分解することです。
「交点を求める」「面積を計算する」など、それぞれのステップを確実に実行していけば、複雑に見える問題も必ず解けるようになります。

つまずいたときはこう考えよう｜やり直しのコツ

「なぜそうなるのか」を言葉で説明できるまで見直しをしよう!

問題が解けないときは、基本に戻る勇気を持ちましょう。
特に重要なのは、自分の理解を言葉で説明できるかどうかです。
「傾きとは何か」「連立方程式の解とは何か」を他の人に説明できるレベルまで理解を深めましょう。

例えば、傾きについて説明するなら「xが1増加したときのyの変化量で、グラフの傾き具合を表す数値」といったように、具体的かつ正確に表現できることが大切です。

また、なぜその解法を選んだのか、なぜその計算をしたのかを自分自身に問いかける習慣をつけましょう。
理由を明確にすることで、同様の問題に遭遇したときの判断力が向上します。

グラフに頼って考えると、計算だけでは見えないことが見えてくる

計算で行き詰まったときは、グラフを描いてみましょう。
グラフは数学的な関係を視覚化する強力なツールです。
特に、解の大まかな値を予想したり、計算結果が妥当かどうかを確認したりする際に威力を発揮します。

例えば、連立方程式を解いて交点の座標を求めた後、実際にその点が両方の直線上にあるかをグラフで確認することで、計算ミスを発見できることがあります。

また、問題の状況をグラフで表現することで、抽象的だった問題が具体的なイメージとして理解できるようになります。

「式だけではわからなかったけれど、グラフを描いたら意味がわかった」という経験を積み重ねることが重要です。

一度理解すれば一生モノ！焦らず着実に積み重ねよう

数学の学習で最も大切なのは、焦らずに着実に理解を積み重ねることです。

一次関数と連立方程式は、その後の数学学習の基礎となる重要な単元ですから、時間をかけてでも確実にマスターしましょう。

理解が曖昧なまま先に進むと、後になって必ずつまずきます。
逆に、ここでしっかりと基礎を固めておけば、中3の二次関数や高校数学にスムーズに進むことができます。

「わからない」と感じたときは恥ずかしがらずに基本に戻り、「わかった」と感じるまで粘り強く取り組みましょう。

一度本当に理解できれば、その知識は一生の財産となります。
数学の面白さや美しさを感じられるようになることでしょう。

まとめ

一次関数と連立方程式は、それぞれ単独で学ぶよりも、「式とグラフをつなげて考える力」を意識することで、理解が飛躍的に深まります。
式の意味をグラフで確かめたり、グラフから式を導き出したりする中で、数学の仕組みが立体的に見えてくるはずです。

また、加減法や代入法のような計算手順も、「なぜこの操作をするのか」と理由まで押さえることが応用力につながります。
そして、困ったときには、グラフに立ち返ることも有効です。
式だけでは見えない関係や、解の妥当性を視覚的に確認できるからです。

大切なのは、覚えた知識をばらばらにせず、式・グラフ・文章題を行き来しながら結びつけていくこと。
この学び方が定着すれば、問題の本質を見抜く力が身につき、数学がより身近で面白いものに感じられるでしょう。